【学术活动预告】Zero capillarity-viscosity limit for an inhomogeneous incompressible fluid model of Korteweg type
时间:2025年5月17日10:40
地点:东校区第二教学楼2106(学术报告厅)
报告人:张志朋 中国海洋大学
报告摘要:
In this talk, we consider the uniform regularity and zero capillarity-viscosity limit for an inhomogeneous incompressible fluid model of Korteweg type in the half-space  , where the velocity satisfies Navier-slip boundary condition and the gradient of density is supplemented with Dirichlet boundary condition. We prove that there exists a unique strong solution of the model in a finite time interval
, where the velocity satisfies Navier-slip boundary condition and the gradient of density is supplemented with Dirichlet boundary condition. We prove that there exists a unique strong solution of the model in a finite time interval 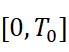 , where
, where  is independent of the capillary and viscosity coefficients, and the solution isuniformly bounded in a conormal Sobolev space. Based on the aforementioned uniform estimates, we further show that the solutions of this model converge to the solution of the inhomogeneous incompressible Euler equations, as the capillary and viscosity coefficients tend to zero simultaneously.
is independent of the capillary and viscosity coefficients, and the solution isuniformly bounded in a conormal Sobolev space. Based on the aforementioned uniform estimates, we further show that the solutions of this model converge to the solution of the inhomogeneous incompressible Euler equations, as the capillary and viscosity coefficients tend to zero simultaneously.
报告人简介:
张志朋,中国海洋大学副教授。主持国家自然科学基金1项。研究方向为流体力学中的偏微分方程,发表论文10余篇。部分研究成果发表在《Calc.Var. Partial Differential Equations》,《SIAMJ. Math. Anal.》,《Nonlinearity》,等期刊上。
